Electrical conductivity 전기 전도도
Electrical conductivity는 어떠한 물체 또는 소재가 electric field 즉 전기장에 반응하는 정도로 정의합니다.
흔히 전기 전도도를 '전기가 잘 통하는 정도'라고 알고 계실 것 같은데요, 일단은 이렇게 이해하셔도 될 것 같습니다.
그리고 어느 물체가 전기장에 잘 반응하면 도체 (Conductor), 잘 반응하지 않으면 부도체 (Insulator), 그리고 애매하게 통하면 반도체 (Semiconductor)라고 부릅니다.
Ohm's Law 옴의 법칙
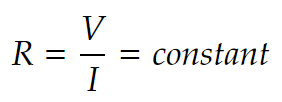
옴의 법칙은 전압(V)과 전류(I)의 비율은 일정하다는 규칙입니다. 따라서 전압과 전류의 비율은 전류의 크기나 방향과는 독립적이라는 것을 알 수 있습니다. 여기서 나오는 전압과 전류의 비를 저항 (electrical resistance)라고 정의합니다.
중요한 포인트는 옴의 법칙은 온도가 일정할 때만 적용할 수 있다는 것입니다. (only at constant temperature)
그리고 사실 많은 물체는 옴의 법칙을 따르지 않습니다. 특히 보통 전류의 크기가 커지면 커질수록 전압과 전류 간의 선형적인 관계가 유지되지 않습니다. 이러한 옴의 법칙을 위배하는 물체를 Non-Ohmic conductors라고 부르며 이러한 물체에 가한 전압을 바꾸면 저항값도 동일하게 유지되지 않습니다.
따라서 옴의 법칙은 '전기 저항값(R)은 전압을 전류로 나눈 값이다'라고 정의하는 규칙이라고 생각하면 될 것 같습니다
Varistors 배리스터
앞서 옴의 법칙을 따르지 않는 소재가 많다고 했는데요, 그중에서도 일부 세라믹 재료는 매우 비선형적인 전압-전류 관계를 갖도록 특별히 설계되었습니다. 이러한 소재를 Variable resistor, 줄여서 배리스터 (Varistor)라고 합니다. (Voltage-dependent resistor (VDR)이라고도 부릅니다)

배리스터의 취지는 어느 전기회로를 고전압 서지로부터 보호하기 위함입니다. 위 그래프를 보시면 ZnO나 SiC는 약 300V의 전압까지는 높은 저항값을 보이다가 전압이 약 300V를 넘기면 저항값이 급격하게 감소하는 것을 볼 수 있습니다. 따라서 배리스터는 지정된 전압(Varistor voltage)을 초과하는 전압 서지가 인가되면 전압을 억제하여 스스로 저항값을 낮추어 회로를 보호합니다.
Conductivity and resistivity 전도도과 저항률
이제 (대부분의 소재가 옴의 법칙을 따른다는 가정하에) 원자적인 레벨에서의 옴의 법칙을 이해해 봅시다.
먼저 전기 저항 (R)은 물체의 길이 (L)와 정비례하며 물체의 단면적 (A)와 반비례합니다. 따라서 전기 저항에 대한 새로운 식을 다음과 같이 세울 수 있습니다.

여기서 ρ는 물체의 고유한 저항력(Resistivity)이며 전기저항 (Resistance)와는 다른 값입니다.
또한 어느 균일적인 물체에 대해서 전기장(Electic field)은 가해진 전압을 물체의 길이로 나눈 값으로 정의되며 (E=V/L) 전류밀도 (Current density)는 전류량을 단면적으로 나눈 값으로 정의됩니다 (J=I/A). 참고로 전기장과 전류밀도 두 값 모두 벡터임으로 크기와 방향 모두 고려해야 됩니다. 따라서 아래와 같이 지금까지 나온 수식을 정리하면 다음과 같이 resistivity (ρ)를 나타낼 수 있습니다.

ρ=E/J라는 식은 여러 방면으로 유용한데요, 먼저 Resistance (R)과 달리 ρ는 물체의 크기에 영향을 받지 않습니다. (L과 A이 약분됨). 즉, ρ는 어느 한 물체의 고유의 값 (혹은 상수)입니다. 그리고 앞서 언급했다시피 ρ는 두 벡터값, 전기장 E와 전류밀도 J와의 관계입니다. 따라서 E와 J는 서로 평행하다는 것을 알 수 있습니다.

이제 resistivity(ρ)의 역수를 위와 같이 전도도 conductivity (σ)로 정의합니다. Resisitivty 그 말대로 어느 물체가 전류의 흐름을 '저항'하는지의 척도였다면 이의 역수인 conductivity는 반대로 어느 물체에 전류가 얼마나 잘 흐르는지를 나타내는 척도입니다. 따라서 conductivity를 사용한 새로운 옴의 법칙인 J= σE를 도출할 수 있습니다.
하지만 새로운 옴의 법칙을 사용하려면 중요한 가정을 해야 되는데요, 바로 물체가 등방성 (isotropic)하는 가정입니다. Isotropic 한 물체는 모든 방향에서 동일한 성질을 보입니다.

위 그림에서 맨 오른쪽 amorphous solid를 나타낸 그림을 보면 결정들이 무작위로 배향된 되어있습니다 (randomly oreinted polycrystals). 이러한 경우에는 물체가 isotropic 하다고 가정할 수 있습니다. 하지만 위 그림에서 왼쪽과 가운데에 있는 single crystal soild와 polycrystal solid와 같이 이방성(anisotropic) 물체에서는 "preferred orientation' 즉, 전류가 선호되는 방향이 존재합니다. 따라서 anisotropic 물체에서는 전류를 어느 방향으로 흐르게 하냐에 따라서 (평행 vs 직각) conducivity가 바뀔 것입니다.
Drude's classical free-electron theory 드루드 모형
Paul Drude라는 과학자는 금속에서 원자당 하나 이상의 원자가 전자가 완전히 비편재화 (delocalized) 돼있고, 이러한 delocalized electrons들은 금속 내부를 기체 입자처럼 돌아다닐 것이라고 가정했습니다. 따라서 드루드는 금속에 있는 전자들이 이상기체처럼 맥스웰-볼츠만 분포 (Maxwell-Boltzmann distribution)을 따르고 전자의 평균 운동에너지 (1/2 mv^2)가 1/2 KbT per degree of freedom와 같을 것이라고 추측했습니다. 여기서 Kb는 볼츠만 상수입니다.
따라서 3차원 금속 속에서 금속표면과 서로에게 충돌하면서 무작위 하게 움직이는 자유 전자의 평균 열 속도 (average thermal velocity)를 다음과 같이 표현할 수 있습니다.

각 상수를 대입해면 온도가 300K일 때 전자의 average thermal velocity는 약 10^5 m/s입니다. 하지만 물체에게 가해진 전기장이 없다면 전자가 금속 속에서 매우 빠른 속도 움직이고 있긴 하지만 전자들은 무작위 한 방향으로 움직이고 선호되는 방향이 없음으로 물체에 흐르는 net current는 존재하지 않습니다.
Drift velocity and charge carrier density 표류 속도와 전하 밀도
이제 금속에 전지장 E가 가해지면 어떠한 일이 벌어지는지 알아봅시다. 전기장 E가 적용되면 금속 속 자유전자들 평균 표류 속도 (Average drift velocity, Vd)와 평균 전류 밀도 (net current density, J)가 생깁니다. 만약 단위 부피당 자유전자의 개수를 전하 밀도 (Ne)라고 정의하면 전류 밀도는 다음과 같이 표현할 수 있습니다.


여기서 꼭 아셔야 되는 부분은 전자의 이동방향과 전기장의 방향이 반대라는 것입니다. 이는 전자가 음전하를 갖기 때문입니다.
Mobility 전자 이동도
이제 우리는 전류 밀도 (J)에 대해서 옴의 법칙을 변형해서 만든 대한 식 (J= σE) 하나와 drift velocity에 관한 식, 이렇게 2개가 있습니다. 이 두 개의 식을 정리하면 다음과 같이 나옵니다.

전하 밀도 (Ne)와 전기장 (E)가 서로 독립적이라고 가정하면 Vd는 E와 정비례할 것입니다.

여기서 우리는 μe를 전자 이동도 (mobility of free electrons)라고 정의합니다.

마지막으로 conductivity 또한 위와 같이 새롭게 정의를 할 수 있습니다. 해당 식을 통해 어느 물체의 전기 전도도는 그 물체의 전하 밀도와 전자 이동도에 의해 결정된다는 것을 알 수 있습니다.
Collision Time
이제 미시적인 관점에서 전자들의 운동을 설명해 봅시다. 먼저 뉴턴의 제2법칙인 F=ma와 전기장으로부터 전자 느끼는 힘이 F=-eE이라는 것은 기억하실 겁니다. 두 식을 조합하면 다음과 같은 관계식을 도출할 수 있습니다.

만약 전자가 완전히 자유롭다면 전자는 위 식과 같이 일정하게 가속할 것입니다. 만약 전자가 가속한다면 전자의 운동에너지 또한 계속해서 커질 것입니다. 하지만 이는 옴의 법칙을 위배하죠. 따라서 드루드는 금속 속의 전자들은 격자 이온 (lattic ions)들과 자주 충돌하며 충돌할 때마다 drift velocity을 잃으며 이를 열로 격자에 전달된다고 가정했습니다.
그러므로 평균 전자 표류 속도 (Average electron dirft velocity)는 전자의 가속도와 충돌 사이의 평균 시간 (collision time or relaxation time)의 곱으로 다음과 같이 나타낼 수 있을 것입니다.

또한 drift velocity와 collision time의 곱은 전자가 충돌 사이에 움직인 평균 거리(Mean free path)를 나타낼 것이며 이는 격자 속 원자(혹은 이온) 간의 거리를 의미할 것입니다.
Hall effect 홀 효과
앞서 배웠다시피 전기 전도도 σ는 σ=e*Ne*μe로 정의할 수 있습니다. 그럼 전하 밀도(Ne)와 전자 이동도(μe)을 따로따로 구할 수 있을까요? 홀 효과 (Hall effect)을 응용하면 구할 수 있습니다.
먼저 자기장 B 내 존자하는 전하량 q를 띄고 있는 입자가 속도 v로 움직일 때 입자가 받는 힘은 F=qv x B 인 것을 기억하실 겁니다.
E.H.Hall이라는 과학자는 아래 그림과 같이 어느 도체 내부에 흐르는 전류(I)의 방향에 수직 한 방향으로 자기장(H)을 가했을 때 도체 속 움직이는 전자들은 전류의 방향과 자기장의 방향에 모두 수직 하는 방향으로 힘(Fm)을 느끼며 해당 방향으로 이동할 것입니다.

따라서 위의 그림 기준으로 전자들은 왼쪽으로 쏠리게 되며 도체의 왼쪽은 - 전하를 띄게 되며 반대편 쪽인 오른쪽에는 전자의 개수가 적어지게 되어 상대적으로 + 전하를 띄게 될 것입니다. 따라서 해당 도체의 양쪽 간의 전위차가 생기게 되며 이렇게 형성되는 전위차를 Hall field (Eh)라고 합니다. Hall field는 자기력 Fm에 반대되는 전기력 (Fe)를 유도하며 두 힘의 방향은 반대이며 크기는 똑같은 평형상태를 유지합니다.

따라서 두 자기력과 전기력의 크기를 같다고 위와 같이 수식을 쓰면 Eh=-RhJB라는 수식을 도출할 수 있습니다. 여기서 Rh는 Hall coefficient입니다.

따라서 위와 같이 Hall coefficient를 사용해 전하 밀도와 전자 이동도를 각각 따로 구할 수 있습니다.
'신소재공학 > 소재 전자기학' 카테고리의 다른 글
| 소재 전자기학 OT (0) | 2024.08.13 |
|---|